斜率是什么意思?从基础到应用的斜率知识大全
大家好呀!今天咱们来聊聊数学中一个超级重要的概念——斜率。说实话,我次听到"斜率"这个词的时候也是一头雾水,感觉特别高大上,但其实它就是一个描述直线倾斜程度的量。下面我就用easy的方式,带大家从基础到应用,全面了解斜率这个神奇的小东西。
斜率的基础概念
斜率,说白了就是一条线有多"斜"。想象一下你走在山坡上,有的坡很陡,有的坡很平缓,斜率就是用来量化这种陡峭程度的数学工具。
在数学上,斜率通常用字母k表示(有时候也用m),它的定义是垂直变化量(y的变化)与水平变化量(x的变化)的比值。用公式表示就是:
k = Δy / Δx = (y₂ - y₁) / (x₂ - x₁)
举个栗子,如果你从点A(1,2)走到点B(3,6),那么x增加了2,y增加了4,斜率就是4/2=2。这意味着y的变化是x变化的两倍。
斜率的几种特殊情况
斜率有一些特别有意思的情况,咱们来看看:
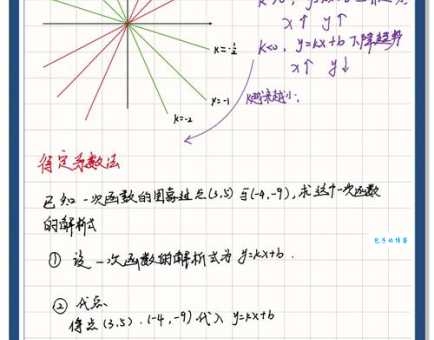
1. 斜率为正:直线从左下向右上倾斜,就像上坡一样
2. 斜率为负:直线从左上向右下倾斜,就像下坡一样
3. 斜率为零:直线完全水平,不倾斜
4. 斜率不存在(无穷大):直线完全垂直,超级陡峭
这里有个小表格总结一下:
| 斜率值 | 直线特征 |
|---|---|
| k > 0 | 向右上方倾斜 |
| k < 0 | 向右下方倾斜 |
| k = 0 | 水平直线 |
| k不存在 | 垂直直线 |
斜率的计算方法
计算斜率其实超级简单,记住"上升比平移"就行了。具体步骤:
1. 在直线上找两个不同的点 (x₁,y₁) 和 (x₂,y₂)
2. 计算y的变化量:y₂ - y₁
3. 计算x的变化量:x₂ - x₁
4. 用y的变化量除以x的变化量就得到斜率
注意哦,x的变化量不能为零,否则斜率就不存在(因为除数为零在数学中是不允许的)。
斜率在直线方程中的应用
斜率常用的地方就是直线方程了。直线的斜截式方程是:
y = kx + b
其中k就是斜率,b是y轴截距(直线与y轴的交点)。知道斜率和截距,直线就完全确定了。
比如y=2x+1,斜率是2,截距是1。这意味着:
1. 每向右移动1个单位,就向上移动2个单位
2. 直线在y轴上的交点是(0,1)
斜率在现实生活中的应用
别看斜率是个数学概念,它在生活中无处不在:
1. 建筑斜坡:轮椅坡道的斜率不能太大,否则轮椅就上不去了
2. 道路设计:高速公路的坡度(斜率)有严格限制,太陡会有安全隐患
3. 经济学:需求曲线的斜率反映了价格变化对需求量的影响程度
4. 物理学:位移-时间图的斜率代表速度
我近装修房子,才发现原来楼梯的设计也要考虑斜率。太陡的楼梯走起来费劲,太缓的楼梯又占空间,所以建筑师要找到一个合适的斜率。
斜率与导数的高级关系
对于曲线来说,每一点的斜率可能都不一样。这时候就要用到微积分中的导数概念了。导数本质上就是曲线在某一点的瞬时斜率。
比如抛物线y=x²,在x=1处的斜率是2(通过求导得到),这意味着在x=1附近,曲线表现得像斜率为2的直线。
这个知识点可能有点进阶,但理解了这个,你就打开了微积分的大门!
斜率的常见误区
学习斜率时容易犯几个错误,我当初也踩过这些坑:
1. 混淆x和y的顺序:斜率是Δy/Δx,不是Δx/Δy
2. 忽略负号:斜率为负表示下降趋势,不能忽略负号
3. 垂直直线的斜率:垂直直线的斜率不存在,不是零
4. 认为斜率大的直线一定"更高":斜率只反映倾斜程度,不反映高度
记住这些,考试时就能避免很多错误啦!
斜率的趣味应用
斜率不只是枯燥的数学概念,它还可以很有趣:
1. 艺术设计:利用不同斜率的线条可以创造动感和节奏
2. 摄影构图:对角线构图的斜率会影响照片的视觉效果
3. 游戏开发:角色跳跃的抛物线轨迹需要精确计算斜率
4. 运动分析:篮球投篮的弧线斜率影响命中率
我玩过一款跑酷游戏,角色在不同斜率的坡道上滑行时速度会变化,这就是斜率在游戏物理引擎中的应用。
总结
斜率这个看似简单的概念,其实蕴含着丰富的数学内涵和广泛的实际应用。从基础的定义到高级的导数关系,从数学题到现实生活,斜率无处不在。希望通过这篇文章,你能对斜率有一个全面而轻松的理解。
后想问问大家,你在生活中还遇到过哪些与斜率相关的例子?有没有哪个斜率的应用让你觉得特别有趣或意外?欢迎分享你的观察和想法!